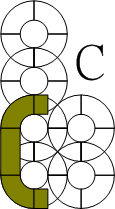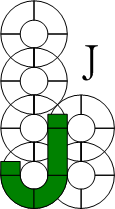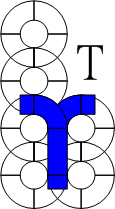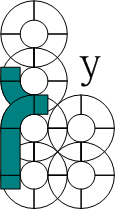
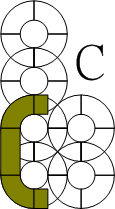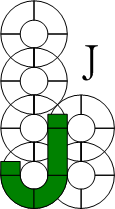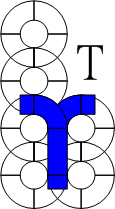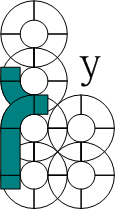

"SEGMENT" has many alias ( and different piece named ) :
Polypleura : projective duals of polyominoes ; connected pieces of the infinite square lattice of edges by Lawrence Detlor.
Polysticks by Brian Barwell.
Polyworms by Livio Zucca Polymultiforms .
See also Ed Pegg Jr. mathpuzzle.com material added 1&10 April 2001.

1999/ 2/ 24 我的父親 (高義勇1923-2004) 拼出來這個最得意,且變化最多的解答( 尚未經考證,計算至 3 個移動元件 )?可以變出16個解答ㄝ!如果您想出來更多的變化請告訴我好嗎?以下有國外刊出來的解答總數,只有 h, J, L, N, y 等五種拼板可以省略不用( 其餘的型片命名些許不同 )。
Total solutions are h: 72 sol. J: 382 sol. L: 607 sol. N: 530 sol. y: 204 sol. from Refereed Papers P159 Dancing Links by Donald E. Knuth P.18
See also Alfred Wassermann Covering the Aztec Diamond with One-sided Tetrasticks. (107 sol.)
I think this solution maybe the most beautiful one. ( i.e. highest symmetry & congruent )


拼板曲線造型係參考專利公報第18卷18期公告編號:161414,證號:066009『益智曲型拼盤』創作人:鄭明顯。但其造型只有10支(C,f,G,h,J,L,u,W,X,y)包圍著 4*4 共16個圓圈,解答數高德納教授 ( P159 Dancing Links by Donald E. Knuth P.24 [1] )說只有83組。
2001/04/23 插入本頁。連結塊的凹槽,參考義大利 Livio Zucca 先生的創新設計雙組32支拼盤。

上下圖用不同的多邊形組成的型片來解答,下圖用正方形及三角形組成最簡單。
這兩個解答也是父親 (高義勇1923-2004) 兩年來閒暇的時候拼出來的成果,與您共享。

參考『數學遊戲大觀』第四集 王登傳 編著,前程出版社 1999年元月再版。第145~148頁:「線巧板」為 陳文錫 先生設計,取名為「智巧板」。刊載有一例解答,也激發了父親 (高義勇1923-2004) 與我不斷地尋求其他解答的興趣。
直到 2001/4/6 才看到 mathpuzzle.com 介紹德國 Alfred Wassermann 先生的作品。原來高德納 ( P159 Dancing Links by Donald E. Knuth P.17 )教授 : The set of all solutions was first found by [37] Bernhard Wiezorke and Jacques Haubrich. (February 1994)

2001/04/23 感謝義大利的 Livio Zucca 先生,運用棋盤著色定理證明:只有 h,J,L,N,y 可以省略。
"The Tetrasticks have parity
problems! To solve the
puzzle, you must eliminate an odd piece
or change the shape." An E-mail from Livio Zucca
2001/4/12. See also his Two
series of TetraSticks.


2002/09/11 父親 (高義勇1923-2004) 又排出來這組 (family) 解答,並列出其相關的鏡射與全等圖形關係。
2002/09/13 首頁的Gif動畫在此列出來,這個家族成員很多,如果僅計算鏡射對稱圖形 (即所謂的 1 個移動圖形元件) 就高達 10 個相關解答;再加上全等的圖形可以兩個對換 (用等號表示全等,算 2 個移動圖形元件) 則有 11 個解答。各位網友不妨挑戰看看是否能超越這個數字?


2001/11/23~25 參加中興大學應數系主辦『國際數學研討會暨第35屆中華民國數學年會』『科技數學組』。講題:『美麗的拼圖 The Most Beautiful Solution』。其中一段.....那麼「甜甜圈」到底要多厚,才能緊密的舖滿一個平面呢?也就是說內圓及外圓要彼此相切。於是應用畢氏定理算出,甜甜圈的厚度是根號2的內圓半徑( SQR(2) * r ) 。(因為 design segment.htm 未更正為 design_segment.htm 造成許多網友來信洽詢說看不到?乾脆把 design_segment.gif 貼到這裡好了)
2005/11/02 補充 segment_rings_overlapped.gif 上圖及頁首的 segment_16pcs_gif.gif 動畫檔。
2005/11/01 ( 2009/01/04 更新鏈結)「線巧板」原創 陳文錫 先生來函告知可參考 科學月刊全文資料庫 (收錄科學月刊 1960年 1月至 1999年 12月共 360期的所有內容) 1975年5月第65期目錄,「線巧板」與「巧體」一文摘錄:『筆者在三年前(民國 61年)曾經設計了一套「線巧板」,取名為「智巧板」(已提出專利申請),該套巧板係由十六片單體組成,每一單體則各由四段單位長度的線段所構成,每一線段與線段之間互成 90°角或 180°角,其全套形狀如第一圖所示。在第二圖中,我們可以見到由其中十五片所組成的一個 5×5方格(為了便於排列,每一塊線巧板的凸轉角處切成 45°)。』